2635. Бикфордов шнур

В прекрасный солнечный день Ёжик прогуливался по своей любимой полянке. Однако, он увидел нечто необычное, чего на полянке раньше не было. Это нечто издали казалось похожим на клубок верёвок. Однако, подойдя поближе, распутав его и изучив материал, из которого он изготовлен, Ёжик пришёл к выводу, что это – бикфордов шнур.

Внимательно посмотрев на него, Ёжик пришёл к выводу, что, похоже что, тому, кто его сделал, было скучно и у него было много свободного времени, так как шнур был запутан, и на нём было завязано огромное количество узлов! После кропотливого пересчёта, выяснилось, что всего имеется n узлов и m соединений между узлами. Каждое из них соединяет два узла и горит равномерно. При поджигании узла загораются все соединения, которые его содержат.

Однако, Ёжику находка не понравилась, и он решил уничтожить её. Для этого он решил использовать так кстати завалявшуюся у него в кармане спичку. Он может поджечь ей один из узлов, и вся эта конструкция начинает гореть. Ёжик – занятой смешарик, и хочет, чтобы эта конструкция сгорела как можно быстрее. Помогите ему определить, какой узел для этого надо поджечь.

Вход. Первая строка содержит два целых числа n и m (2 ≤ n ≤ 100, 1 ≤ m ≤ n·(n – 1) / 2) – количество узлов и веревок между узлами, соответственно.

Следующие m строк содержать описания соединений между узлами – три целых числа a_i, b_i и t_i (1 ≤ a_i, b_i ≤ n, a_i ≠ b_i, 1 ≤ t_i ≤ 1000) – номера узлов, которые соединяет i-ая веревка и за сколько секунд эта веревка полностью сгорит, будучи подожжённой с одного из концов.

Каждую пару узлов соединяет максимум одна веревка. Гарантируется, что весь шнур может сгореть, если поджечь любой его узел.

Выход. Выведите пару чисел – номер узла, который надо поджечь, и за какое время при этом сгорит весь шнур.

Пример входа	Пример выхода
4 4 1 2 3 2 3 4 1 3 5 1 4 1	2 4

РЕШЕНИЕ

графы – алгоритм Флойда-Уоршела

Анализ алгоритма

Пусть g – матрица расстояний заданного графа. Вес ребер графа равен времени сгорания веревок. По условию задачи весь шнур может сгореть, поэтому граф связный. Ищем кратчайшие расстояния между всеми парами вершин при помощи алгоритма Флойда – Уоршела.

Если поджечь узел (вершину графа) v, то вся конструкция веревок сгорит через время, равное расстоянию от вершины v до самой дальней вершины. Остается найти вершину, расстояние от которой до самой дальней минимально.

Пример

Ниже приведен граф из примера и матрица кратчаших расстояний.

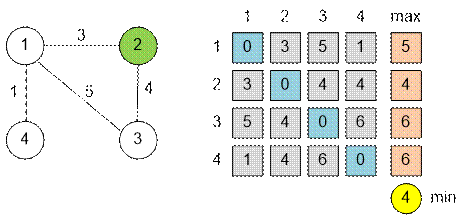
При поджеге вершины 2 все остальные вершины сгорят бытрее всего, а именно за 4 секунды.

Реализация алгоритма

Матрицу расстояний храним в массиве g.

#define MAX 102

int g[MAX][MAX];

Читаем входные данные. Строим граф g. Вершины нумеруются числами с 1 до n.

scanf("%d %d",&n,&m);

memset(g,0x3F,sizeof(g));

for(i = 1; i <= n; i++) g[i][i] = 0;

for(i = 1; i <= m; i++)

scanf("%d %d %d",&a, &b, &len),

g[a][b] = g[b][a] = len;

Запускаем алгоритм Флойда – Уоршела поиска кратчайших путей между парами вершин.

floyd();

Совершаем поджог вершины i (1 ≤ i ≤ n). Находим расстояние max от нее до самой дальней вершины. Среди всех вычисленных значений max находим наименьшее значение min.

min = 0x3F3F3F3F;

for(i = 1; i <= n; i++)

{

max = 0;

for(j = 1; j <= n; j++)

if (g[i][j] > max) max = g[i][j];

if (max < min) min = max, node = i;

}

Выводим номер узла node, который следует поджечь, и минимально возможное время min сгорания всех веревок.

printf("%d %d\n",node,min);